Identificação com a massa!
Atenção! Está prestes a ir ao fundo de alguns conceitos físicos importantes!
Numa forma mais completa da fórmula de massa-energia de Einstein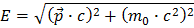 
, E é a energia da partícula, p é o seu momento e m0 é a sua massa em repouso. Acontece que esta definição de massa é invariante na Natureza, denominada a “massa invariante”. Trabalhando a fórmula obtemos:
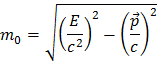
Como esta quantidade é invariante, e baseada em quantidades que se conservam (a Energia e o momento), podemos utilizá-la para reconstruir a massa da partícula que decai: mede-se a energia e momento dos produtos de decaimento e, dado que o que entra tem que sair, obtém-se a Energia e o momento da partícula “mãe”, e daí a sua massa. Bastante direto e simples, não é?
No caso de um Bosão Z decair num par electrão (e-) positrão (e+), a soma das energias e dos momentos do electrão e do positrão leva-nos à massa do Bosão Z da seguinte maneira:
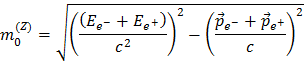
A energia e o momento do bosão Z, EZ=Ee- + Ee+ e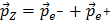 
, são determinados porque o detetor ATLAS pode medir a energia e o momento dos seus produtos de decaimento. Isto quer dizer que tem tudo o que precisa para calcular a massa do bosão Z ou de outras partículas como o J/ψ and e o Υ!
De facto, este método da massa invariante funciona para uma variedade de combinações de produtos de decaimento, como γγ, l+l- (l=e,μ), l+l-l+l- e outros, conforme irá descobrir quando estudar o bosão Z, procurar o bosão de Higgs, ou as usar mesmo para explorar o desconhecido!