Vectors
You might notice that there is an arrow over the momentum: 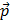 . You remember that the everyday definition of momentum is speed times mass:
. You remember that the everyday definition of momentum is speed times mass: 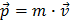 and you see that the speed also is marked with an arrow. This means that the quantity is a vector. And by a vector we mean that it has a magnitude (a size), and a direction in space. This is natural, since if you have a speed of a certain magnitude you are at the same time heading off in a certain direction. When performing mathematical operations with vectors we have to treat them with care. We have to decompose the vector which points in some arbitrary direction in space, to how much it points into some chosen (projection) direction x, y and z of our coordinate system. So a multiplication between two momenta will be a scalar, i.e. a number without direction:
and you see that the speed also is marked with an arrow. This means that the quantity is a vector. And by a vector we mean that it has a magnitude (a size), and a direction in space. This is natural, since if you have a speed of a certain magnitude you are at the same time heading off in a certain direction. When performing mathematical operations with vectors we have to treat them with care. We have to decompose the vector which points in some arbitrary direction in space, to how much it points into some chosen (projection) direction x, y and z of our coordinate system. So a multiplication between two momenta will be a scalar, i.e. a number without direction:
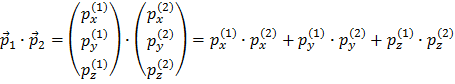
There are no components which mixes one direction with the other, since these are just 0. Also notice that there are no arrows over the resulting terms. This is because the (scalar) product of two vectors is just a number (a scalar), which means it has no direction.