Momentum
In everyday life, momentum is defined as the mass times the velocity of some object: 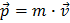 . However, at the LHC all the particles both before and after the collisions travel close to the speed of light (v=0,999999991c for accelerated protons). You therefore have to use the theory of special relativity of Einstein, and the formula for momentum is a bit more complicated but still manageable.
. However, at the LHC all the particles both before and after the collisions travel close to the speed of light (v=0,999999991c for accelerated protons). You therefore have to use the theory of special relativity of Einstein, and the formula for momentum is a bit more complicated but still manageable.
We start out with Einsteins famous formula
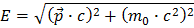
Here E stands for energy, p for momentum, m for mass and c for the speed of light. Momentum is a vector with three projections on three axes (x,y,z), and if you do not know what a vector is, follow Vectors.
If you do a bit of algebra (simple shuffling around of the formula’s arguments) you can express the magnitude of momentum as function of energy and mass:
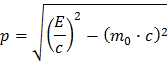
In nature, momentum is conserved. This means: What goes in must come out, which in our particle collisions means that pbefore=pafter. For a Z boson decaying to an electron-positron pair this would mean pZ = pe- + pe+.
Quiz-question: In the everyday-life version of momenta p=mv we encounter a problem with massless objects like the photon, their momentum would be 0. What happens with the momentum in case of a massless particle in the special relativity version of momentum?