Pęd
W życiu codziennym momentum definition określany jest jako masa razy prędkość jakiegoś obiektu: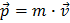 
.
Jednakże, w akceleratorze LHC wszystkie cząstki, zarówno przed jak i po zderzeniu, poruszają się z prędkością prawie równą prędkości światła (v=0,999999991c dla przyspieszonych protonów). Trzeba zatem użyć Szczególnej Teorii Względności Einsteina i wzór na pęd staje się trochę bardziej skomplikowany.
Zaczniemy od słynnego wzoru Einsteina:
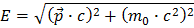
Tutaj E oznacza energię, p - pęd, m - masę, a c - prędkość światła. Pęd jest wektorem o trzech składowych wzdłuż osi (x, y, z). Więcej o wektorach można przeczytać w rodziale Wektory.
Po dokonaniu prostych przekształceń algebraicznych (przeniesienia zmiennych we wzorze) można wyrazić pęd przez energię i masę:
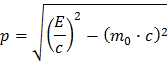
W przyrodzie pęd jest zachowywany, co oznacza, że całkowity pęd przed zderzeniem i po zderzeniu musi byc taki sam: pprzed= ppo. Dla bozonu rozpadającego się na parę elektron-pozyton mamy: pZ = pe- + pe+.
Pytanie testowe: przy stosowaniu definicji pędu z życia codziennego, p=mv, napotykamy na problem z cząstkami bezmasowymi takimi jak foton. bo ich pęd byłby równy zeru. Co dzieje się z pędem dla takich cząstek w Szczególnej Teorii Względności?