Ορμή
Στην καθημερινή μας ζωή, η ορμή ορίζεται ως η μάζα επί την ταχύτητα ενός αντικειμένου: 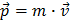 . Στον LHC όμως, όλα τα σωματίδια και πρίν και μετά τις συγκρούσεις ταξιδεύουν με ταχύτητες σχεδόν ίσες με την ταχύτητα του φωτός (v=0,999999991c για τα πρωτόνια). Πρέπει λοιπόν να χρησιμοποιήσεις την Ειδική Θεωρία της Σχετικότητας του Αϊνστάιν, και η σχέση που δίνει την ορμή θα είναι λίγο πιο πολύπλοκη αλλά βατή.
. Στον LHC όμως, όλα τα σωματίδια και πρίν και μετά τις συγκρούσεις ταξιδεύουν με ταχύτητες σχεδόν ίσες με την ταχύτητα του φωτός (v=0,999999991c για τα πρωτόνια). Πρέπει λοιπόν να χρησιμοποιήσεις την Ειδική Θεωρία της Σχετικότητας του Αϊνστάιν, και η σχέση που δίνει την ορμή θα είναι λίγο πιο πολύπλοκη αλλά βατή.
Ξεκινάμε με το γνωστό τύπο του Αϊνστάιν:
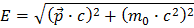
Το σύμβολο Ε αντιστοιχεί στην ενέργεια, το p στην ορμή, το m στην μάζα και το c στην ταχύτητα του φωτός. Η ορμή είναι διανυσματικό μέγεθος, και αν δεν θυμάσαι τι είναι διάνυσμα πήγαινε στα διανύσματα.
Με λίγες αλγεβρικές πράξεις μπορείς να εκφράσεις την ορμή ως συνάρτηση της ενέργειας και της μάζας:
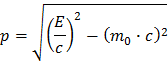
Στη φύση, η ορμή διατηρείται. Δηλαδή: εισερχόμενη και εξερχόμενη ορμή είναι ίσες. Οπότε pπριν=pμετά. Για τη διάσπαση του σωματιδίου Z σε ζευγάρι ηλεκτρονίου-ποζιτρονίου αυτό σημαίνει pZ = pe- + pe+.
Ερώτηση: Με τον "καθημερινό" ορισμό της ορμής p=mv έχουμε πρόβλημα με τα άμαζα σωματίδια (για παράδειγμα το φωτόνιο). Η ορμή τους θα είναι μηδέν. Τι ακριβώς γίνεται στην ειδική θεωρία της σχετικότητας ως προς αυτό το θέμα;